
Bienvenido al Análisis de SHA-3
Esta página presenta una exploración interactiva y visual del algoritmo criptográfico SHA-3, el estándar de hash más moderno desarrollado por NIST.
A través de demostraciones animadas y ejemplos prácticos, descubrirás cómo funciona la construcción Sponge, las permutaciones Keccak-f, y las ventajas de seguridad que hacen de SHA-3 una alternativa robusta a SHA-2.
Construcción Sponge: Visualización Animada
Observa cómo SHA-3 absorbe y exprime datos en tiempo real
- •Estado público visible
- •Vulnerable a ataques de extensión de longitud
- •Tamaño de salida fijo
- •Diseño más tradicional
- •Capacity oculta (seguridad interna)
- •Inmune a ataques de extensión
- •Salida de longitud variable (XOF)
- •Diseño completamente diferente
- 1.El mensaje se divide en bloques de r bits
- 2.Cada bloque se XOR con la parte rate del estado
- 3.Se aplica la función de permutación Keccak-f[1600]
- 4.Se repite hasta procesar todo el mensaje
- 1.Se extraen r bits del estado como salida
- 2.Si necesitamos más bits, aplicamos Keccak-f[1600]
- 3.Repetimos hasta obtener el tamaño de hash deseado
- 4.Para SHA3-256, solo necesitamos 256 bits
Simplicidad
Un solo algoritmo para cualquier tamaño de salida
Seguridad
Resistente a ataques de extensión de longitud
Flexibilidad
Salida de longitud variable (XOF)
Paralelizable
Se puede implementar eficientemente en hardware
Padding en SHA-3: Preparando el Mensaje
Comprende cómo se completan los bloques con el esquema pad10*1
El mensaje se divide en bloques del tamaño adecuado para el algoritmo. Si el mensaje no es múltiplo del tamaño de bloque, se le agrega padding (relleno) para completar. SHA-3 usa el esquema pad10*1: un 1, luego los 0 necesarios, y se cierra con 1.
El padding se calculará automáticamente para SHA3-224 (rate = 1152 bits)
Cómo funciona la función f

La función f es donde ocurre toda la mezcla interna del algoritmo.
Podemos pensar el estado de f como un volumen tridimensional de datos, formado por 1.600 bits organizados en una matriz de 5×5×64.
Cada posición en ese volumen representa una parte del estado, y sobre este espacio tridimensional se aplican las operaciones de mezcla —las cinco transformaciones: θ,ρ,π,χ eι— que actúan sobre filas, columnas y planos del cubo para lograr una difusión completa de los bits a lo largo de todo el estado.
Estructura 3D del Estado:
- • 5×5×64 = 1600 bits totales
- • 25 lanes de 64 bits cada uno
- • 24 rondas de transformación
Permutaciones de Keccak-f
Las 5 operaciones que transforman el estado en cada ronda
Theta
Operación 1 de 5
Calcula, para cada bit, el XOR entre ese bit y una combinación de las columnas vecinas (la columna actual y las adyacentes, con aritmética módulo 5 en los índices). En la práctica, se obtiene el XOR de cada columna completa y ese resultado se propaga a las columnas vecinas. Con esto, la información "salta" a lo largo de las columnas y se difunde rápidamente por todo el estado, iniciando la mezcla global.

Nota: Estas cinco operaciones se ejecutan en secuencia (θ → ρ → π → χ → ι) formando una ronda completa. Keccak-f[1600] aplica 24 rondas para lograr la difusión y confusión necesarias para la seguridad criptográfica.
Eficiencia de Keccak-f
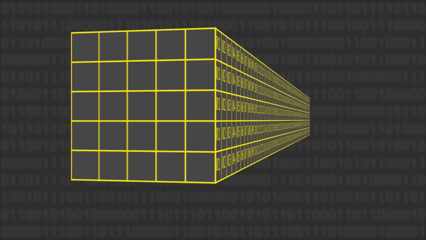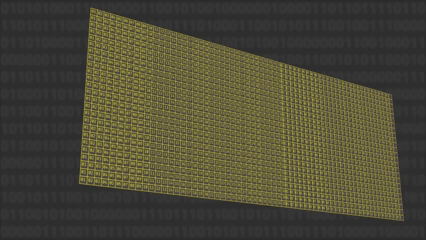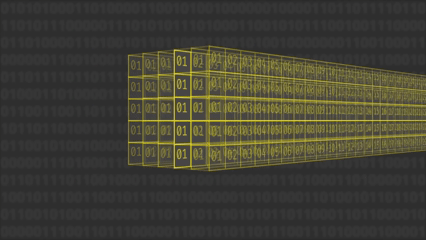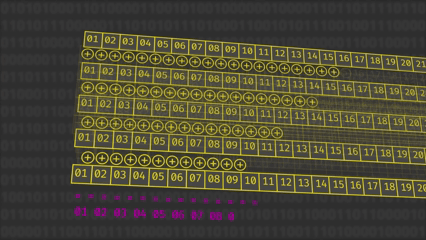
Aunque se puede pensar en el rate y capacity como un "volumen" 5×5×64, en la práctica no se guarda como un cubo de bits. Se representa como 25 palabras de 64 bits (un arreglo 5×5 de "lanes", cada lane es un int64): en total 25×64 = 1600 bits del estado de Keccak-f.
Esta representación hace que las operaciones de cada ronda sean muy eficientes porque se aplican a nivel de palabra:
θ (theta): los XOR de "columnas" se calculan como XOR de cinco palabras de 64 bits cada una (una por lane de la columna). Eso da el "parity" de columna en una sola operación por palabra, sin extraer bits individuales.
ρ (rho): es solo un rotate de 64 bits por lane (las CPUs tienen rotaciones de palabra muy rápidas).
π (pi): es reindexar/mover referencias: cada palabra pasa a otra posición (permuta las 25 palabras).
χ (chi): se implementa con operaciones binarias entre palabras: A[i] ^= (~A[i+1]) & A[i+2] (índices módulo 5 dentro de la fila), todo en 64 bits de ancho.
ι (iota): un XOR de la constante de ronda directamente sobre una de las palabras.
Como los índices se toman módulo 5, para "vecinos" basta referenciar otra palabra del arreglo (no hay que manipular bits sueltos).
Conclusión: al modelar el estado como 25 uint64, se evitan operaciones lentas de "enmascarar y desplazar" bits. Casi todo se reduce a XORs, ANDs y rotaciones entre 25 variables, lo que hace a Keccak muy amigable al hardware y también eficiente en software.
Comparación de Velocidad: SHA-2 vs SHA-3
Análisis de rendimiento entre ambos algoritmos
Resistencia al Length Extension Attack
SHA-3 es inmune a este tipo de ataque por diseño
H(mensaje) puede calcular H(mensaje || padding || datos_extra) sin conocer el mensaje original. SHA-3, gracias a su construcción sponge, es naturalmente resistente a este ataque.- El atacante conoce el hash
H(mensaje_secreto)pero no el mensaje - En SHA-2, el hash es el estado interno después de procesar el mensaje
- El atacante puede "continuar" el hasheo añadiendo datos extras
- Esto compromete esquemas como
H(clave_secreta || mensaje)
Efecto Avalancha
Pequeños cambios producen resultados completamente diferentes